Teorema de convolución
De Wikipedia, la enciclopedia libre
En matemática, el teorema de convolución establece que bajo determinadas circunstancias, la Transformada de Fourier de una convolución es el producto punto a punto de las transformadas. En otras palabras, la convolución en un dominio (por ejemplo el dominio temporal) es equivalente al producto punto a punto en el otro dominio (es decir dominio espectral).Sean f y g dos funciones cuya convolución se expresa con
 . (notar que el asterisco denota convolución en este contexto, y no multiplicación; a veces es utilizado también el símbolo
. (notar que el asterisco denota convolución en este contexto, y no multiplicación; a veces es utilizado también el símbolo  ). Sea
). Sea  el operador de la transformada de Fourier, con lo que
el operador de la transformada de Fourier, con lo que ![\mathcal{F}[f]](http://upload.wikimedia.org/wikipedia/es/math/d/7/d/d7d873880ca971775d26eb69f3367046.png) y
y ![\mathcal{F}[g]](http://upload.wikimedia.org/wikipedia/es/math/d/a/b/dabdbab1b4cd473f71aa2deb3c5efaa0.png) son las transformadas de Fourier de f y g, respectivamente.
son las transformadas de Fourier de f y g, respectivamente.Entonces
 , podemos escribir:
, podemos escribir:[editar] Demostración
La demostración funciona para normalizaciones unitarias y no unitarias de la transformada de Fourier, pero en la versión unitaria tiene factores extras de que son inconvenientes aquí. Sean
que son inconvenientes aquí. Sean 
Sean F la transformada de Fourier de f y G la transformada de Fourier de g:

 .
.
 , así que su transformada de Fourier está definida. Sea H la transformada de Fourier de h:
, así que su transformada de Fourier está definida. Sea H la transformada de Fourier de h: y gracias al argumento de arriba podemos aplicar nuevamente el teorema de Fubini:
y gracias al argumento de arriba podemos aplicar nuevamente el teorema de Fubini:![\mathcal{F}[f*g]=\sqrt{2\pi} (\mathcal{F}[f]) \cdot (\mathcal{F}[g])](http://upload.wikimedia.org/wikipedia/es/math/6/8/b/68b2b101fce265a2c9c244a19a6c882c.png)
![\mathcal{F}[f \cdot g]=\frac{\mathcal{F}[f]*\mathcal{F}[g]}{\sqrt{2\pi}}](http://upload.wikimedia.org/wikipedia/es/math/0/7/d/07dcb8c430d9f9bcbd7454b9f3302570.png)
![f*g=\sqrt{2\pi} \mathcal{F}^{-1}[\mathcal{F}[f]\cdot\mathcal{F}[g]]](http://upload.wikimedia.org/wikipedia/es/math/4/b/8/4b828cedb4c0446539c258232aa97281.png)



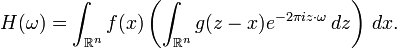





No hay comentarios:
Publicar un comentario